In this video, I derive the following identitiessin(x) = 2*t / (1 t^2)cos(x) = (1 t^2) / (1 t^2)These identities are important when it comes to simpli3 The formula cos2A = cos2 A−sin2 A We now examine this formula more closely We know from an important trigonometric identity that cos2 Asin2 A = 1 so that by rearrangement sin2 A = 1− cos2 A So using this result we can replace the term sin2 A in the double angle formula This givesCombine Like Terms Solve for a Variable Factor Expand Evaluate Fractions Linear Equations Prove that \sin x\tan x>2x, when 0

Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube
Tan 2x formula in terms of sin x
Tan 2x formula in terms of sin x-Three examples are that (1) any trigonometric expression can be converted to an expression in terms of only sin and cos, (2) expressions involving exp(x) can be converted to their hyperbolic forms, and (3) a trigonometric function with an argument of the form q Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions sin –t = –sin t cos –t = cos t tan –t = –tan t Sum formulas for sine and cosine sin (s t) = sin s cos t cos s sin t cos (s t) = cos s cos t – sin s sin t Double angle formulas for sine and cosine sin 2t = 2 sin t cos t



Power Reducing Formulas And How To Use Them With Examples Owlcation
9/9/ · Answer Formulas that express the trigonometric functions of an angle 2x in terms of functions of an angle x at trigonometric formulae are known as the double angle formulae They are called 'double angle' because they consist of trigonometric functions of double angles, ie, sin 2A, cos 2A, and tan2A We can start with the additional formulae of the double angle formulae for sinSolve for x tan (2x)=1 tan (2x) = 1 tan (2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan (1)3/1/18 · First, we recall `tan x = (sin x) / (cos x)` `tan a/2=(sin a/2)/(cos a/2)` Then we use the sine and cosine of a half angle, as given above `=sqrt((1cos a)/2)/sqrt((1cos a)/2)` Next line is the result of multiplying top and bottom by `sqrt 2` `=sqrt((1cos a)/(1cos a))`
Proofs of Trigonometric Identities I, sin 2x = 2sin x cos x Joshua Siktar's files Mathematics Trigonometry Proofs of Trigonometric Identities Statement $$\sin(2x) = 2\sin(x)\cos(x)$$Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1Values of x at which tanx is undefined, tanx has both left and right vertical asymptotes Specifically, if a is a value of x outside the domain of tanx, then lim x!a¡ tanx = 1 and lim x!a tanx = ¡1 † Cotangent The function cotx is a lot like tanx It is defined at all values of x for which sinx 6= 0 In other words, the domain of
The most straightforward way to obtain the expression for cos(2x) is by using the "cosine of the sum" formula cos(x y) = cosx*cosy sinx*siny To get cos(2 x ), write 2x = x x Then, · If you're doing this by de Moivre, the trick is to keep the form you get from initially expanding (CiS)^3, (where C = cos x, S = sin x) rather than rewriting to get sin 3x in terms of only sin x ie (CiS)^3 = C^3 3i C^2S 3 C S^2 iS^3 So sin 3x =3 C^2 S S^3, cos 3x = C^33CS^2 And Then just divide by C^3 to rewrite in terms of tan xI wanted to find $\tan2x$ in terms of $\cos x$ alone I was able to do it in terms of $\sin x$ alone $\tan2x = \sin2x/\cos2x$ Since, $\cos2x = 12\sin^2x$ Therefore, $\tan2x = (\sin2x / 12\sin^2x)$ Is it possible to do it in terms of $\cos x$ alone ?



Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download



5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download
2/12/ · Ex 33, 23 Prove that tan4𝑥 = (4 tan〖𝑥 (1−tan2𝑥)〗)/(1 − 6 tan2 𝑥tan4 𝑥) Taking LHS tan 4x We know that tan 2x = (2 𝑡𝑎𝑛𝑥)/(1 − 𝑡𝑎𝑛2 𝑥) Replacing x with 2x tan (2 × 2x) = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) tan 4x = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) = (2 taThey are Arc cos x, Arc tan x, Arc cot x, Arc sec x, and Arc csc xUsing following trigonometric identities Sinx^2Cosx^2==1 Sinx/Cosx==Tanx Cscx==1/Si Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers



Solve The Equation On Interval 0 2p Tan2x Sin X Tessshebaylo
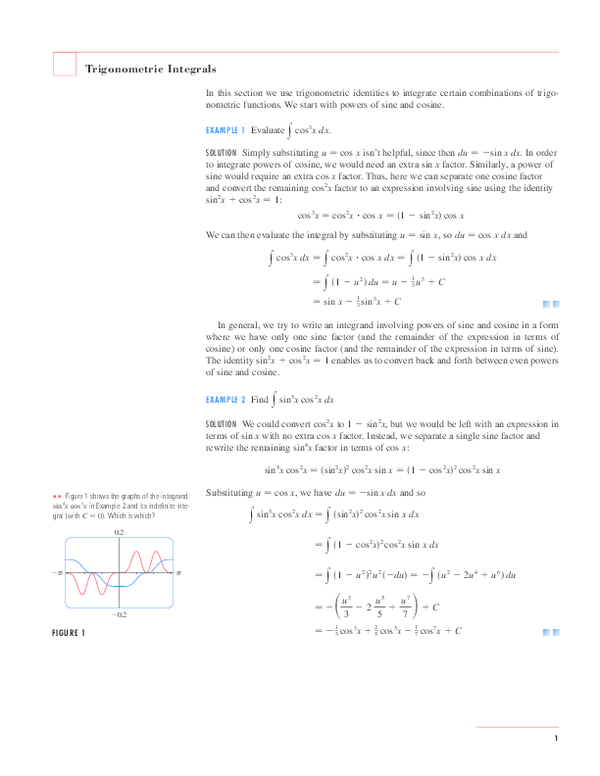


Pdf Trigonometric Integrals Jerome Delen Academia Edu
11/21/19 · Recall the double angle formula cos(2x) = cos^2(x) – sin^2(x) We also know the trig identity sin^2(x) cos^2(x) = 1, so combining these we get the equation cos(2x) = 2cos^2(x) 1 Now we can rearrange this to give cos^2(x) = (1cos(2x))/2 So we have an equation that gives cos^2(x) in a nicer form which we can easily integrate using theA formula can often be simplified, as was found by deriving the tangent formulas from the sine and cosine formulas, and changing it from terms using one ratio to terms using another ratio In doing this, the Pythagorean theorem, expressed in trigonometry ratios, is very handy Assume that a right triangle has a hypotenuse of 1 unit longAnd also to tan ( 3 x) = − tan ( x) 4 sin 2 ( x) − 3 − 4 sin 2



Trigonometric Functions With Their Formulas



Trig Identity Sec2x Minus Tan2x T10 Youtube
5/17/16 · tan 2x = ((2sin x)/(1 2sin^2 x))sqrt(1 sin ^2 x) sin 2x = (sin 2x)/(cos 2x) Applying the 3 trig identities sin 2x = 2sin xcos x , and cos 2x = (1 2sin^2 x) cos x = sqrt(1 sin^2 x) We get tan 2x = (2sin xcos x)/(1 2sin^2 x) = = ((2sin x)/(1 2sin^2 x))sqrt(1 sin^2 x)This equation is true at x = 60° and, by the symmetry of the tangent curve, also at x = 180° 60° = 240° In radians , this is The second factor solves asDerive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes \(tan(aa) =\frac{ tan a tan a }{1 tan a tana}\) \(Tan 2a =\frac{2tan a}{1tan^{2}a} \) Practice Example for tan 2 theta Question



Sum And Difference Identities Video Lessons Examples And Solutions



Solved Section 7 3 Double Angle Half Angle And Product Chegg Com
11/2/16 · For each expression in column I, choose the expression from column II to complete an identity Column I Column II 1 tanxcosx A sin^2x/cos^2x 2 sec^2x1 B 1/sec^2x 3 sec x/cscx C sin(x) 4 1sin^2x Dcsc^2xcot^2xsin^2x 5To rewrite the sine function in terms of tangent, follow these steps Start with the ratio identity involving sine, cosine, and tangent, and multiply each side by cosine to get the sine alone on the left Replace cosine with its reciprocal function Solve the Pythagorean identity tan 2After doing so, the first of these formulae becomes sin(x x) = sin x cos x cos x sin x so that sin2x = 2 sin x cos x And this is how our first doubleangle formula, so called because we are doubling the angle (as in 2A) Practice Example for Sin 2x If we want to solve the following equation We will follow the following steps



Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
· Solution Solve for x in the given equation Arc tan (2x)arctan(x)=π/4 Solution Evaluate arc cot 2cos (arc sin 05) Solution Arc tan 2cos (arc sin (3^(1/2) / 2)) is equal to12/7/15 · How to Write Double Angle Formula sin 2x in terms of tan x4/14/16 · #tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x#, for the right hand side expression Explanation #2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x)#
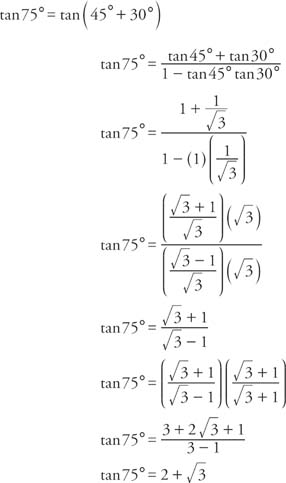


Tangent Identities



If Cos 2x Cos 4x 1 Then Tan 2x Tan
3/31/ · The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle Source enwikipediaorg Derivation of the FormulaApplying the quotient rule to the definition of the tangent as the quotient of the sine by the cosine, one gets that the tangent function verifies d d x tan x = 1 tan 2 x {\displaystyle {\frac {d}{dx}}\tan x=1\tan ^{2}x}To see the answer, pass your mouse over the colored area To cover the answer again, click "Refresh" ("Reload")



Cos X Plus Sin X Upon Cos X Minus Sin X Minus Cos X Minus Sin X Upon Cos X Plus Sin X Is Equal To 2 Brainly In
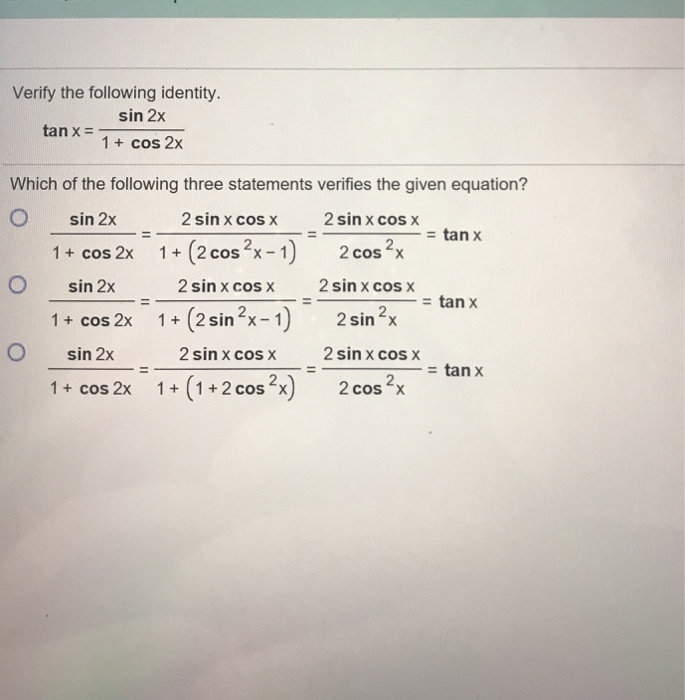


Solved Verify The Following Identity Tan X Sin2x 1 Co Chegg Com
12/27/19 · The word 'trigonometry' being driven from the Greek words' 'trigon' and 'metron' and it means 'measuring the sides of a triangle' In this Chapter, we will generalize the concept and Cos 2X formula of one such trigonometric ratios namely cos 2X with other trigonometric ratios Let us start with our learning!2/22/21 · Tan2x Formulas Tan2x Formula = 2 tan x 1 − t a n 2 x We know that tan (x) = sin (x)/cos (x) Then, tan2x formula = sin (2x)/cos (2x) Tan 2x can also be written in terms of sin x and cos x, Tan2x Formula in terms of cos x = 2 s i n ( x) c o s ( x) c o s 2 x − s i n 2 xπ, where q is a rational, can in some cases be converted to
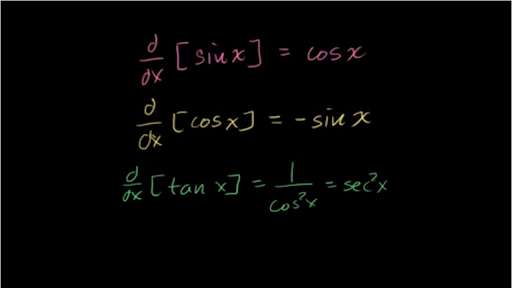


Derivatives Of Sin X Cos X Tan X Eˣ Ln X Video Khan Academy



Find Sin 2x Cos 2x And Tan 2x If Sinx 5 13 And X Terminates In Quadrant I Ala Sin 2x U H Cos Brainly Com
The second shows how we can express cos θ in terms of sin θ Note sin 2 θ "sine squared theta" means (sin θ) 2 Problem 3 A 345 triangle is rightangled a) Why?Cos 2x = (1tan^2 x)/(1 tan^2 x)` Plugging `tan x = sqrt6/3` in the formulas above yields11/2/14 · sin2x = 2 sinx cosx and sin(2(x)x) = sin 2x cos x sinx cos 2x using the last two identities gives sin3x= 2 sinx cosx cosx sinx cos2x factoring the sinx we have sin3x = sinx(2cosx cosxcos2x)
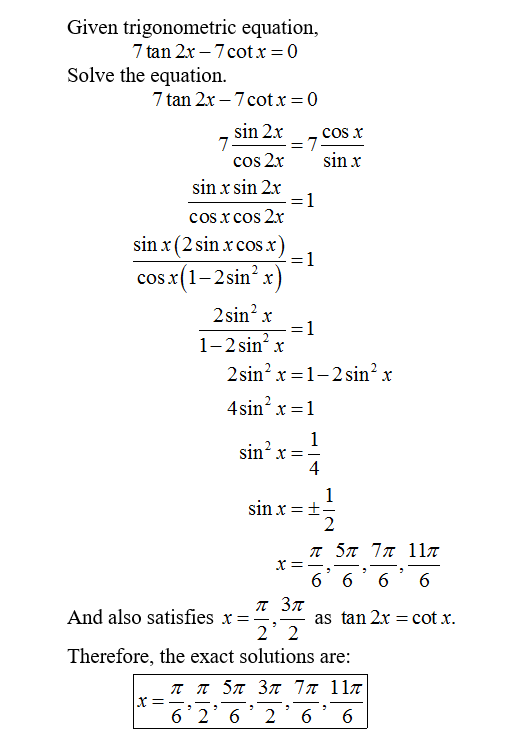


Solved Given Trigonometric Equation 7 Tan 2x 7 Cotx Chegg Com



Math34 Trigonometric Formulas
Sin(2X) = 2 sinX cosX cos(2X) = 1 2sin 2 X = 2cos 2 X 1 tan(2X) = 2tanX / 1 tan 2 X Multiple Angle Formulas sin(3X) = 3sinX 4sin 3 X cos(3X) = 4cos 3 X 3cosX sin(4X) = 4sinXcosX 8sin 3 XcosX cos(4X) = 8cos 4 X 8cos 2 X 12/26/21 · Formula of Trigonometry – Sin, Cos, Tan, Cot, Sec & Cosec February 27, 21 February 26, 21 by self s Formula of Trigonometry Trigonometry is a well acknowledged name in the geometric domain of mathematics, which is in relevance in this domain since ages and is also practically applied across the number of occasions1/30/07 · Homework Statement seems simple, but i am stumped Says write cos(x) in terms of tan(x) Homework Equations would this be a reciprocal equation?



Derivative Of Tan 2x 3 From First Principle Brainly In


Derivatives Of Trigonometric Functions
You need to write sin 2x and cos 2x in terms of tanx such that `sin 2x = (2 tan x)/(1 tan^2 x);The Pythagorean formula for tangents and secants There's also one for cotangents and cosecants, but as cotangents and cosecants are rarely needed, it's unnecessary Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and9/25/09 · Sin2x= Tan2x*Cos2x but note that Cos^2(2x)=1/Sec^2(2x) using sec^2(2x)=1 tan^2(2x) we then get Sin2x=Tan2x/Sqrt(1tan^2(2x)) this is all ok but sin2x=2sinxcosx so you need to do the same for cos2x and find cosx in terms of tan2x thus replace it into the expression above



Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
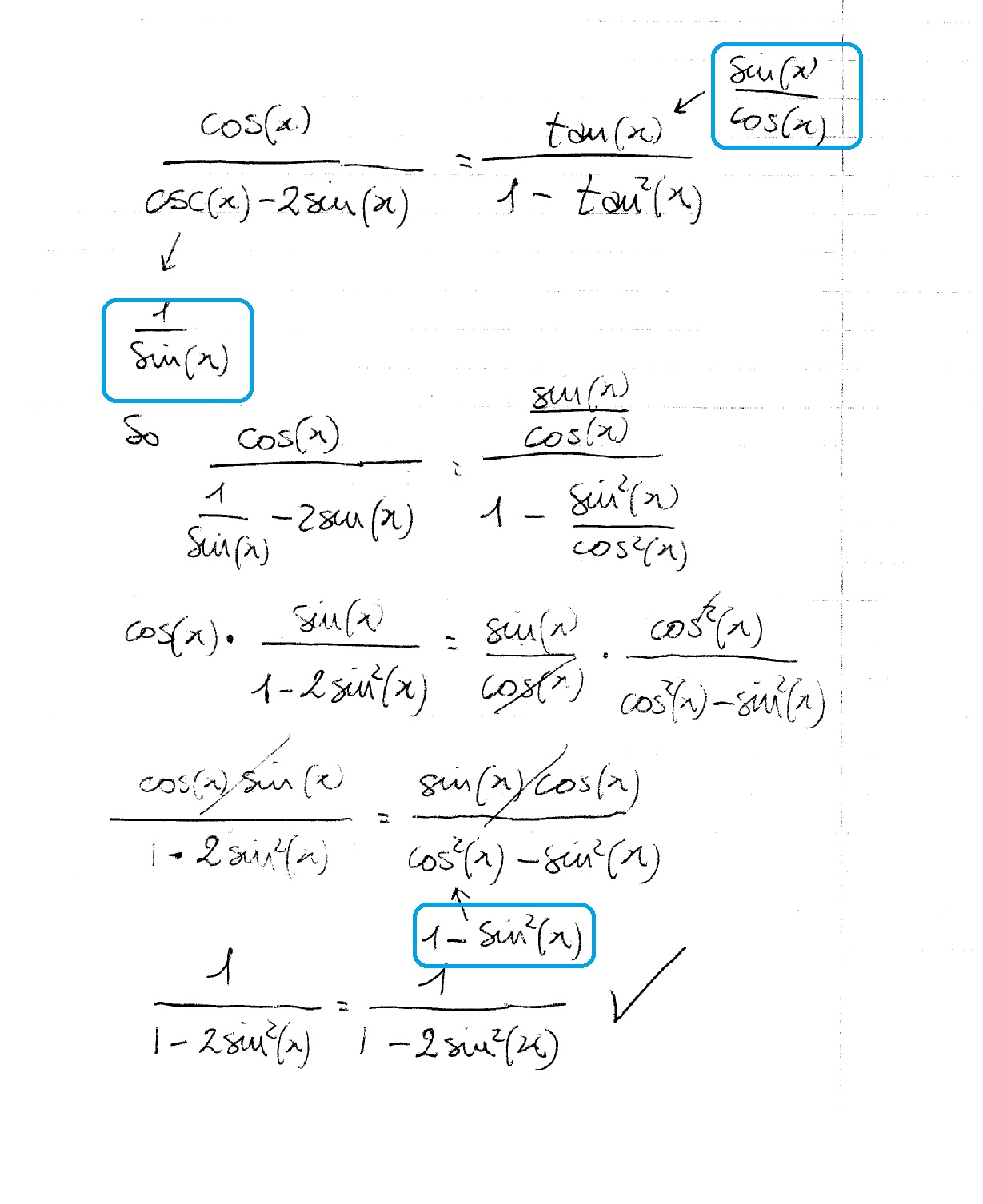


How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic
It is also used to simplify the quotient of the subtraction of tan squared of angle from one by the sum of one and tan squared of angle as the cosine of double angle $\implies$ $\dfrac{1\tan^2{\theta}}{1\tan^2{\theta}}$ $\,=\,$ $\cos{2\theta}$ Other forms In the cosine double angle formula, the angle can be represented by any symbolX There aren't any terms or factors involving in this formula, so let's make up another one An equivalent formula for is math\implies\tan^2x=\dfrac {\sin^2x\sin^2x\cos^2x} {\sin /math Continue Reading There aren't any terms or factors involving in this formula, so let's make up another one An equivalent formula for isThe equation x = sin y defines y as a multiplevalued function of x This function is the inverse of the sine and is symbolized Arc sin x The inverse functions of the cosine, tangent, cotangent, secant, and cosecant are defined in a similar way;



Power Reducing Formulas And How To Use Them With Examples Owlcation



How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
Trigonometry Solve for x sin (2x)=tan (x) sin(2x) = tan(x) sin ( 2 x) = tan ( x) Rewrite tan(x) tan ( x) in terms of sines and cosines sin(2x) = sin(x) cos(x) sin ( 2 x) = sin ( x) cos ( x) Rewrite the equation as sin(x) cos(x) = sin(2x) sin ( x) cos ( x) = sin ( 2 x)The first shows how we can express sin θ in terms of cos θ;12//16 · To get the formula for tan 2A, you can either start with equation 50and put B = A to get tan(A A), or use equation 59for sin 2A / cos 2nd divide top and bottom by



Powers Of Trigonometric Functions



Solved Problem 4 Using The Sin And Cos Addition Formulas Chegg Com
A half turn, or 180°, or π radian is the period of tan(x) = sin(x) / cos(x) and cot(x) = cos(x) / sin(x), as can be seen from these definitions and the period of the defining trigonometric functions5/12/21 · Misc 15 sin(tan−1 x), 𝑥 < 1 is equal to (A) 𝑥/√(1 − 𝑥2) (B) 1/√(1 − 𝑥2) 1/√(1 𝑥2) (D) 𝑥/√(1 𝑥2) Let a = tan−1 x tan a = x We need to find sin a For this first we calculate sec a and cos a We know that sec2 a = 1 tan2 a sec a = √(1𝑡𝑎𝑛2 a) We convert tI'm lost The Attempt at a Solution i dont even know where to begin



Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube



Trigonometric Integrals Geogebra



Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified



Tan 2x Formula Learn Formula For Calculating The Double Angle Tan 2x
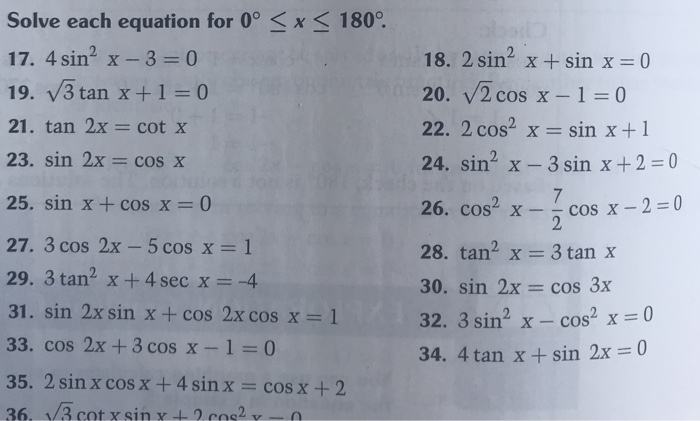


Solved Solve Each Equation For 0 X 180 17 4 Sin2 X Chegg Com


What Is The Formula Of Tan2x Quora



Inttanx Tan2x Tan3x Dx Is Equal To



14 2 Trigonometric Identities



If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx



Section 7 3 Double Angle And Half Angle Formulas Flashcards Quizlet
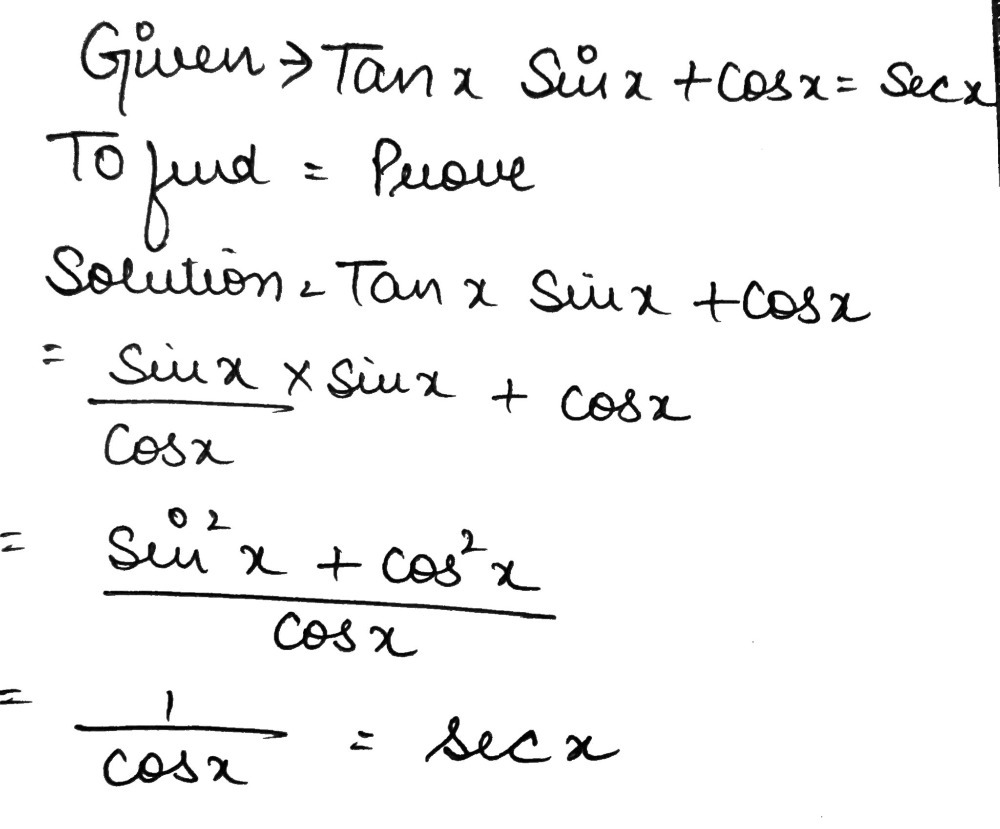


Zed Biqb4zbq9m



Solve The Following Equation Tan X Tan 2x Tan 3x 0



Weierstrass Substitution Wikipedia



Tan2x Formula In Terms Of Tan Edurev Class 12 Question


What Are The Formulas Of Cos 2x Quora


What Is The Identity Tan 2x Equal To In Terms Of Sinx And Cosx Quora



1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube



Integrate Tan 2x By Parts



Old Version Show Sin 2x 2 Sin X Cos X 2tan X 1 Tan 2 X Youtube
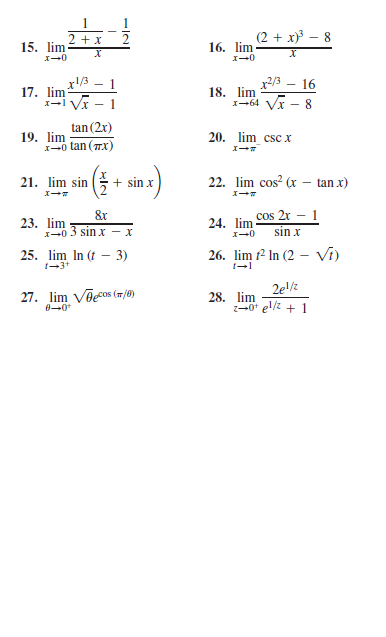


Answered X 2 X 8 15 Lim 16 Lim X2 3 Bartleby



Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube



7 3 Exercises



Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube



The Derivative Of Tan 2x Derivativeit



Trigonometric Integrals



Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2



Math34 Trigonometric Formulas
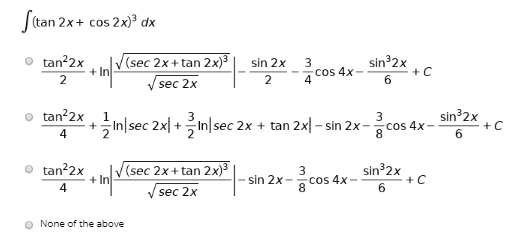


Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby


Tan2x ただの悪魔の画像



Dana Harrington Benjamin Leis Thanks So Much For Responding But I Don T Think That S The Case All 6 Solutions Work In The Original Equation When Subbed In Also When You Graph



If Sin X 5 3 And 0 Lt X Lt P 2 Find The Value Of Sin 2x Cos 2x Tan 2x Brainly In


Solved A First Rewrite The Left Hand Side 1 Tan 2x In Terms Of Sin X And Cos X B Next Add The Two Terms In The Expression You Got In Part


Is Tan 2x Equal To Tan X 2


Differentiate The Following From First Principles I Tan 2 X Ii Tan 2x 1 Sarthaks Econnect Largest Online Education Community



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55



Section 7 3 Double Angle Half Angle And Sum


7 Proving Ids Trig Functions Identities



2sinxcosx Identity Gamers Smart


What Is The Formula Of Tan2x Quora
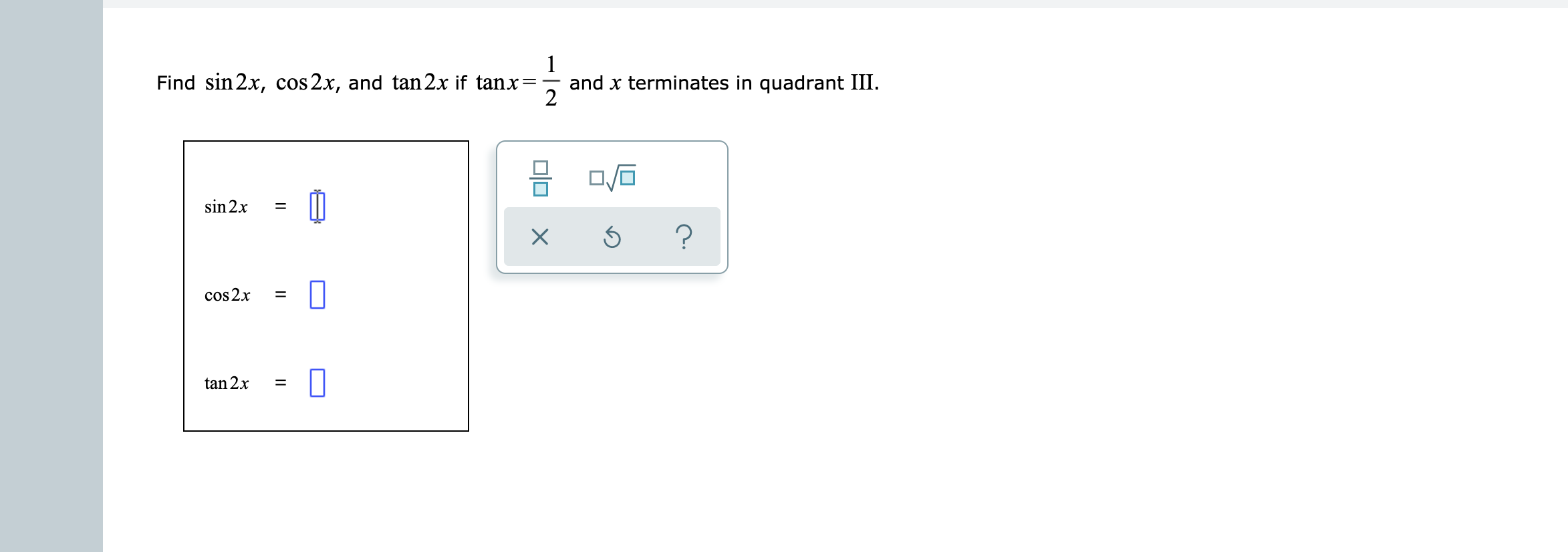


Answered 1 Find Sin 2x Cos 2x And Tan 2x If Bartleby
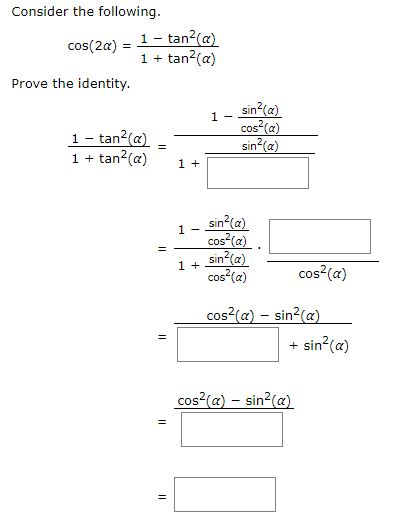


Solved Prove The Identity 2 Tan X Sin 2x 1 Tan2x Wr Chegg Com



What Is Integral Of Sin2x Tan2x Quora


Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities
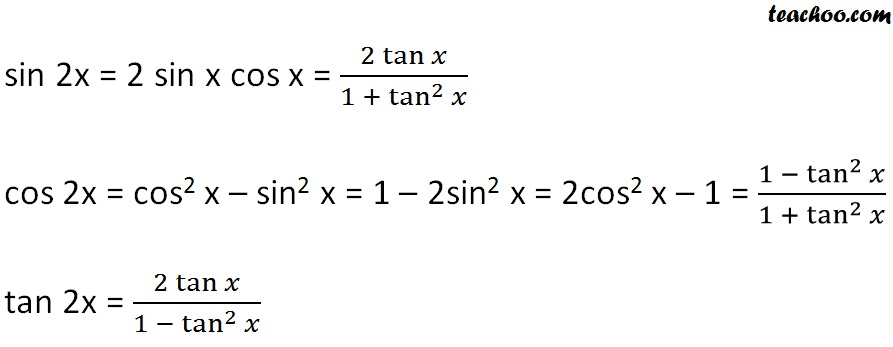


Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi


If Cos X 1 2 Then What Is The Value Of Tan 2x Quora



Tangent Half Angle Formula Wikipedia



Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2


8 Solve The Equation Sec C22x See How To Solve It At Qanda



Double Angle Properties Rules Formula Examples Video Lesson Transcript Study Com



Sin 2 2x Cos 2 2x Learn Lif Co Id
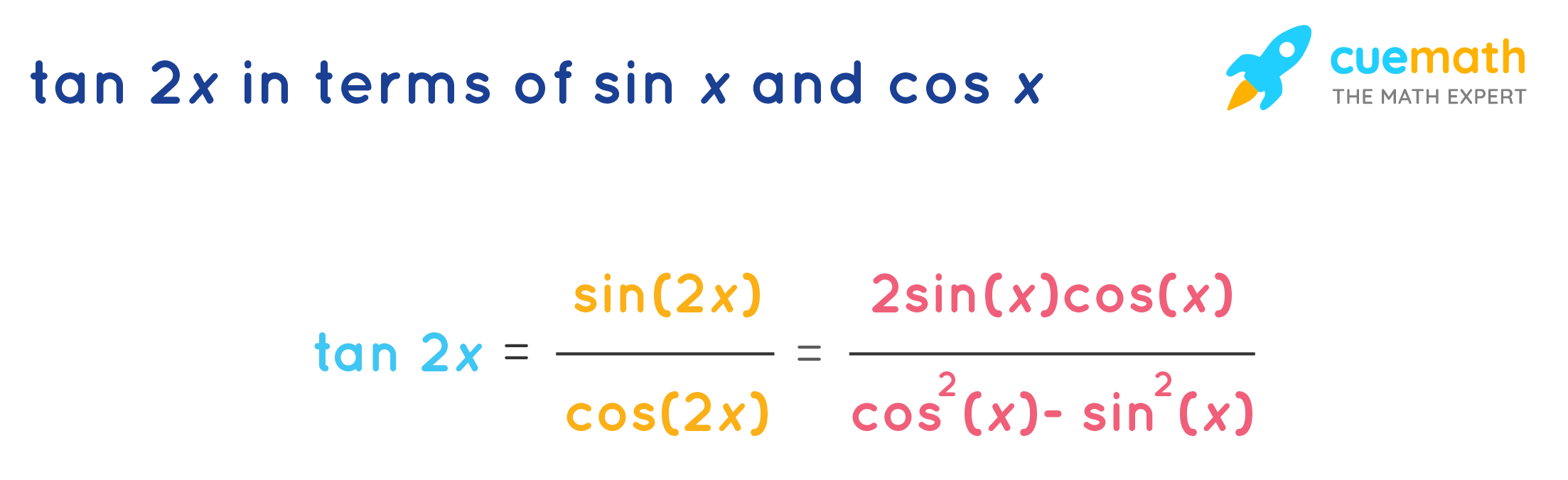


Tan 2x Formula Learn Formula For Calculating The Double Angle Tan 2x



Howto How To Find Vertical Asymptotes Of Tan2x
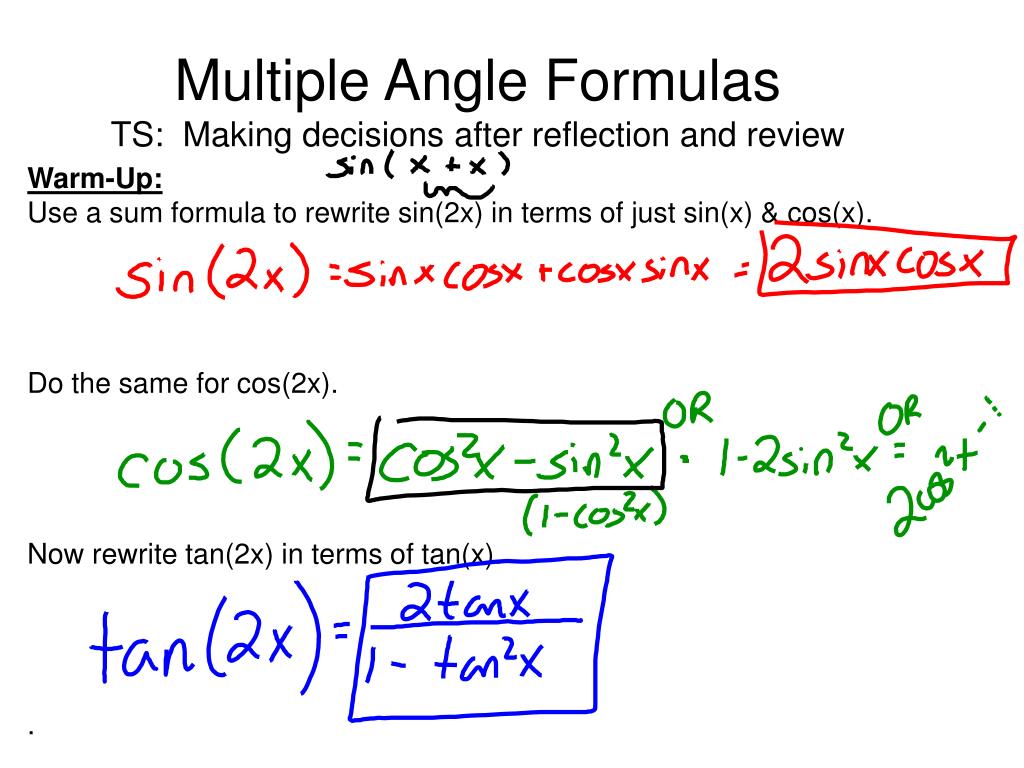


Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id



How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic



Tangent Half Angle Formula Wikipedia



14 2 Trigonometric Identities



How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



Use Identities To Rewrite Cosx Sinxtanx In Terms Of Sin X And Cos X Then Simplify So That No Quotients Appear Wyzant Ask An Expert



Ex 3 3 19 Prove Sin X Sin 3x Cos X Cos 3x Tan 2x



How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



If Y Tan X Tan 2x Tan 3x Sin 12x 0 Then Dy Dx Has The Va



Tangent Half Angle Formula Wikipedia



Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction


What Is The Formula Of Tan2x Quora


Trig Find Tan X Given Tan 2x 2 Pi X 3pi 2 Cheatatmathhomework



Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help



0 件のコメント:
コメントを投稿